Multiply − 1 1 by 0 0 Add 16 16 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k kShare It On Facebook Twitter Email 1 Answer 1 vote answered by Shyam01 (504k points) selected by Chandan01 Best answer As the sum of distances of any point P on the ellipse from the two foci is equal to the length of the major1 The square of the length of the tangent from (3, 4) to the circle x^2y^24x8y 3 = 0 is 2 If (x, y) and (3, 5) are the extremities of a diameter of a circle with centre at (2, 3), then the values of x and y are 3 The equation 2x^2 2y^2 4x 8y = 15 = 0 represents 4
1
16^(x^2+y)+16x+y^2)=1
16^(x^2+y)+16x+y^2)=1-Simple and best practice solution for x=(1/2)(168y) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSolve for x Multiply both sides of the equation by , the least common multiple of 16,625 Multiply both sides of the equation by 1 0 0 0 0, the least common multiple of 1 6, 6 2 5 Add 16y^ {2} to both sides Add 1 6 y 2 to both sides Divide both sides by 625




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange
Click here👆to get an answer to your question ️ If 2^2x y = 32 and 2^x y = 16 then x^2 y^2 is equal to Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables > Algebraic Methods of Solving a Pair of Linear Equations > If 2^2x y = 32 and 2^x maths If 2 2 x − y = 3 2 and 2 x y = 1 6 then x 2 y 2 is equal to A 9 B 1 0 C 1 1 D 1 3 Medium AnswerIf a chord of the parabola y 2 = 4 a x, passing through its focus F meets it in P and Q, then ∣ F P ∣ 1 ∣ F Q ∣ 1 = View solution If ( x 1 , y 1 ) and ( x 2 , y 2 ) and end of a focal chord of the parabola y 2 = 4 a x , then square of G6y4xy 6y − 4xy View solution steps Short Solution Steps \frac { 36 y 16 x ^ { 2 } y } { 2 ( 2 x 3 ) } 2 ( 2 x 3) 3 6 y − 1 6 x 2 y Factor the expressions that are not already factored Factor the expressions that are not already factored \frac {4y\left (
16(x 2 2x 1) – 9(y 2 – 4y 4) – 16 36 – 164 = 0 16(x 2 2x 1) – 9(y 2 – 4y 4) – 144 = 0 16(x 1) 2 – 9(y – 2) 2 = 144 Here, center of the hyperbola is (1, 2) So, let x 1 = X and y – 2 = Y The obtained equation is of the form Where, a = 3 and b = 4 Eccentricity is given by Foci The coordinates of the foci are (±ae, 0) X = ±5 and Y = 0 x 1 = ±5Find all $x, y \in \mathbb{R}$ such that $$16^{x^2 y} 16^{x y^2} = 1$$ The first obvious approach was to take the log base $16$ of both sides If P is a point on the ellipse x 2 /16 y 2 /25 = 1 whose foci are S and S′, then PS PS′ = 8 conic sections;
Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 24x^3(y2)16x^2(2y)16x(y2) so that you understand betterStep 1 Equation at the end of step 1 (16 • (x 2)) (2 2 •3 2 y 2) Step 2 Equation at the end of step 2 2 4 x 2 (2 2 •3 2 y 2) Step 3 Step 4 Pulling out like terms 41 Pull out like factors 16x 2 36y 2 = 4 • (4x 2 9y 2) Trying to factor as a Difference of Squares 42 Factoring 4x 2 9y 2To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If the curves `x^2/alphay^2/4=1 and y^2=16 x` intersect at right angles, then



1




Answers
Click here👆to get an answer to your question ️ Find all pairs (x, y) of real numbers such that 16^x^2 y 16^x y^2 = 1 Transcript Ex 114, 1 Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola x2 16 y2 9 = 1 Given equation is 2 16 2 9 = 1 The above equation is of the form 2 2 2 2 = 1 So axis of hyperbola is xaxis , Comparing (1) & (2) a2 = 16 a = 4 & b2 = 9 b = 3 Now, c2 = a2 b2 c2 = 16 9 c2 = 25 c = 5 Coordinate of ∴ 16 x^2 y 16 y^2 y = 1 The equality holds when (x 1/2) 2 (y 1/2) 2 = 0 x = – 1/2 & y = – 1/2 is the only solution Therefore the pair is (1/2, 1/2) secondarymath Post navigation MCQ WORKSHEET, POLYNOMIALS PROBLEM Write the value of x for which 2x, x 10 and 3x 2 are in AP Leave a Reply Cancel reply Your email address will not be published



1




No Links Please Q 15 Find The Area Included Between The Parabola Y2 16x And The Line Joining Its Vertex Maths Relations And Functions Meritnation Com
For this hyperbola Find the center, transverse axis, vertices, foci, and asymptotesIntegration multivariablecalculus Share Cite Follow edited Dec 14 '19 at 946 TheHolyJoker 1,927 1 1 gold badge 6 6 silver badges 24 24 bronzeGraph 16x^2y^2=16 16x2 y2 = 16 16 x 2 y 2 = 16 Find the standard form of the ellipse Tap for more steps Divide each term by 16 16 to make the right side equal to one 16 x 2 16 y 2 16 = 16 16 16 x 2 16 y 2 16 = 16 16 Simplify each term in the equation in order to set the right side equal to 1 1




Find The Area Bounded By The Cirxle X 2 Y 2 16 And The Line Y X In The First Quadrant Youtube




Free Math Answers Answers Within 24 Hours Step By Step Explanations
Precalculus Geometry of a Hyperbola Graphing Hyperbolas 1 Answer Narad T The16x^28xyy^2 This deals with factoring multivariable polynomials Overview; x y = 1 y = x1 (1) x^2 y^2 = 16 (2) Substituting (1) into (2) x^2 (x1)^2 = 16 x^2 x^2 2x 1 = 16 2 x^2 2x 15 = 0 Solving the quadratic equation for x, x= (sqrt31 1) /2 or (sqrt31 1) /2 Substituting x into (1) to find y, y = (sqrt31 1) /2 or (sqrt31 1) /2 Algebra Science Anatomy & Physiology Astronomy Astrophysics Biology Chemistry Earth




How Do You Use The Shell Method To Set Up And Evaluate The Integral That Gives The Volume Of The Solid Generated By Revolving The Plane Region About The Y Axis Given Y 16x X 2



What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora
Simple and best practice solution for (y^27xy16x^2)dxx^2dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework I solved the question using double integral $$\int_{4}^{4}\int_{\sqrt{(16x^2)}}^{\sqrt{(16x^2)}} \frac{16x^2y^2}{4}dydx$$ the answer I'm getting is $32\pi$ but my book answer is $16\pi$ What am I doing wrong? (x^2y^21)^3x^2*y^3"=0>Je ne vois pas le rapport entre cette équation et la saint Valentin>Peutêtre sa représentation graphique Or la représentation graphique dessinée est un coeur Estce que la représentation graphique de cette fonction est vraiment un coeur ?




The Height Of A Ball In Feet Is Modeled By Tex Y 16x 2 72x Tex Where X Is The Time In Brainly Com
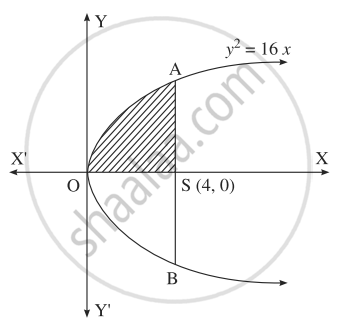



Find The Area Of The Region Bounded By The Parabola Y2 16x And Its Latus Rectum Mathematics And Statistics Shaalaa Com
We can rewrite this as follows 16x^29y^232x144y16=0 (Multiply with 1 both sides) 16*(x^22x)9(y^216y)16=0 16*(x^22x1)9(y^)()=0 16*(x1)^29*(y8)^2=576 (y8)^2/64(x1)^2/36=1 ((y8)/8)^2((x1)/6)^2=1 Finally the standard form for the hyperbola is (y(8))^2/8^2(x1)^2/6^2=1 If we plot it on the cartesian plane it isUnlock StepbyStep x^2/16y^2/16z^2/16=1 Extended Keyboard Examples16 x ^ { 2 } y ^ { 2 } 1 1 6 x 2 y 2 − 1 Rewrite 16x^{2}y^{2}1 as \left(4xy\right)^{2}1^{2} The difference of squares can be factored using the rule a^{2}b^{2}=\left(ab\right)\left(ab\right)




X 2dy Y 2 7xy 16x 2 Dx 0 When X 1 Y 1 Youtube




The Equation Of Projectile Is Y 16x X 2 4 The Horizontal R
Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value − 2 2 into f ( x) = 4 √ − 1 x 1 f ( x) = 4 1 x 1 In this case, the point is ( − 2, ) (Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSimple and best practice solution for X2y=16 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,




Find The Roots Of Quadratic Equation 16x 2 24x 1 0 By Using Quadratic Formula Brainly In



Chapter 1 Real Numbers And Algebra 1 1
Topics Terms and topics; 16 (x 2 2xy y 2) 4 2 (x 2 2xy y 2) 4 2 (x y) 2 = 4 (xy) (4 x y ) = 4 x y) (4 x y) HOPE YOU UNDERSTOOD!!! If the tangent at (1, 7) to the curve x 2 = y – 6 touches the circle x 2 y 2 16x 12y c = 0 then the value of c is (1) 195 (2) 185 (3) 85 (4) 95 jee;
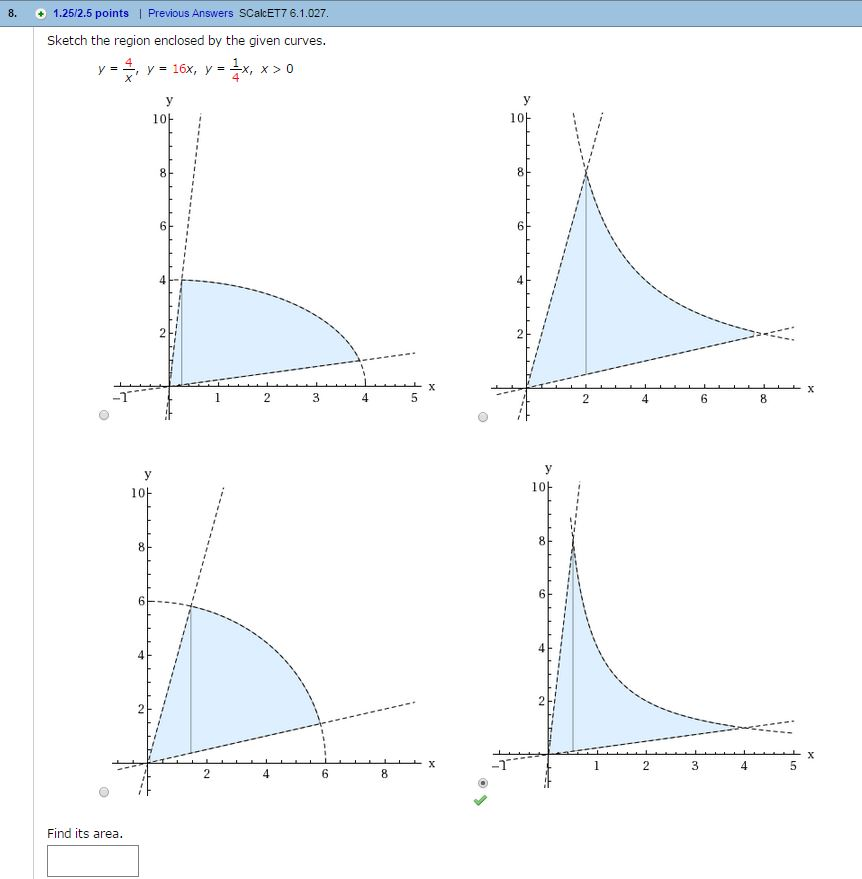



Sketch The Region Enclosed By The Given Curves Chegg Com




Find Domain And Range Of Function Y 1 X 2 16 Youtube
Et comment faire pour dessiner une équation de ce type (via un petitGraph (x^2)/4 (y^2)/16=1 x2 4 − y2 16 = 1 x 2 4 y 2 16 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1 x2 4 − y2 16 = 1 x 2 4 y 2 16 = 1 This is the form of a hyperbola Use this form to determine theEquations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 16x^22xyy^2 so that you understand better



Determine The Length Of The Chord Common To The Circle X 2 Y 2 64 And X 2 Y 2 16x 0 Quora



Solution Please Im Asking For Your Guys Devine Help Your Assisstance Would Be Very Very Important To Me So Please Offer Me A Helping Hand 1 Find The Foci Of An Ellipse With The Equation
Learn with Tiger how to do 16x^2y^2/xy/4/y1/x fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, Reducing (Simplifying) Fractions Tiger Algebra SolverSolution for 16xy^2=0 equation Simplifying 16x 1y 2 = 0 Solving 16x 1y 2 = 0 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add 'y 2 ' to each side of the equation 16x 1y 2 y 2 = 0 y 2 Combine like terms 1y 2 y 2 = 0 16x 0 = 0 y 2 16x = 0 y 2 Remove the zero 16x = y 2 Divide each side by '16' x = y 2 Find the values of ^2 y^2/4 = 1 and y^3 = 16x cut each other orthogonally ← Prev Question Next Question → 0 votes 410k views asked in Limit, continuity and differentiability by SumanMandal (546k points) Find the values of 2 y 2 /4 = 1 and y 3 = 16x cut each other orthogonally the tangent and normal;




Identify And Sketch The Surface 16x 2 Y 2 2z 2 Chegg Com



16x 2 4y 2 32x 16y 32 0 Find The Ellipse Mathskey Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreY = − x 2 16 y = x 2 16 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 16 a = 1 16 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down Find the vertex ( h, k) ( h, k)Click here👆to get an answer to your question ️ The foci of the ellipse x^2/16 y^2/b^2 = 1 and the hyperbola x^2/144 y^2/81 = 1/25 coincide Then the value of b^2 is



Solved Find The Particular Solution Indicated For The Following Course Hero




Mpm2d Systems Of Linear Equations Test 2
Share It On Facebook Twitter Email 1 Answer 1 vote answered by rubby (5k points) selected by Vikash Kumar Best answer Ans 4 Solution ← Prev Question Next Question →Simple and best practice solution for xy=16 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for xy=16 equation Simplifying x 1y = 161 solution(s) found (4xy)^2 (4xy)^2 See steps Step by Step Solution Step 1 Equation at the end of step 1 (2 4 x 2 8xy) y 2 Step 2 Trying to factor a multi variable polynomial 21 Factoring 16x 2 8xy y 2 Try to factor this multivariable



How Do You Solve The Following By Quadratic Equation For X Given 15x 2 16xy 15x 2 0 Socratic



2
If the foci of the ellipse x^2/16 y^2/b^2 = 1 coincide with the foci of the hyperbola x^2/144 y^2/81 = 1/25, asked in Mathematics by Nakul (701k points) jee;Click here👆to get an answer to your question ️ If the curves x^2a^2 y^24 = 1 and y^3 = 16x intersect at right angles, then a^2 is equal to Join / Login > 12th > Maths > Application of Derivatives > Tangents and Normals > If the curves x^2a^2 y^ maths If the curves a 2 x 2 4 y 2 = 1 and y 3 = 1 6 x intersect at right angles , then a 2 is equal to A 5 / 3 B 4 / 3 C 6 / 1 1 It is clear that 16 − x 2 ≤ 16, which is tight Then a square root is nonnegative, and you immediately get 0 ≤ 16 − x 2 ≤ 16 = 4 All values in that range can be reached, because the equation y = 16 − x 2 has solutions for all y ∈ 0, 4 (one such solution is x = 16 − y 2 )



How To Solve The System X 2 Y 2 25 And Y 3 4x Quora




Number Of Real Solutions Of X 4 8x 2 16 4x 2 12 X 9 Youtube
0 votes 1 answer The foci of a hyperbola coincide with the foci of the ellipse x^2/25 y^2/9 = 1 Find the equation of the hyperbola, asked in Mathematics by Sindhu01 (571k points) How do you graph #y^2/16x^2/4=1# and identify the foci and asympototes?16^(x²y) 16^(y²x) = 1 (1) Equation (1) is only and only possible when 16^(x²y) = 1/2 and 16^(y²x) = 1/2 Then 1/2 1/2 = 1 Take 1st part 16^(x²y



What Will Be The Domain And The Range Of The Equation Y 1 Sqrt 16 X 2 Quora




Rd Sharma Solutions For Class 8 Chapter 9 Linear Equation In One Variable Download Free Pdf
Crosses at y=4 As this equation is already in the correct format, put x and y equal to zero and you will see that when x=0, y^2=16 which gives the y intercepts If you put y=0, you get x^2=9 which doesn't give any real roots The graph will therefore be a hyperbola in the shape of a V and an upside down V (as opposed to being on their sides like >Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Ppt 4 X 2 2 X Y 2 8 4 Powerpoint Presentation Free Download Id




Answered 0 Is Cnte Raph Costai Function 229en Bartleby




F X X 3 X 2 16 X X 2 2 X 2k K X 2 Find The Value Of K So That The Followi Youtube




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange



2




Solution What Is The Focus Of The Parabola Y 2 16x
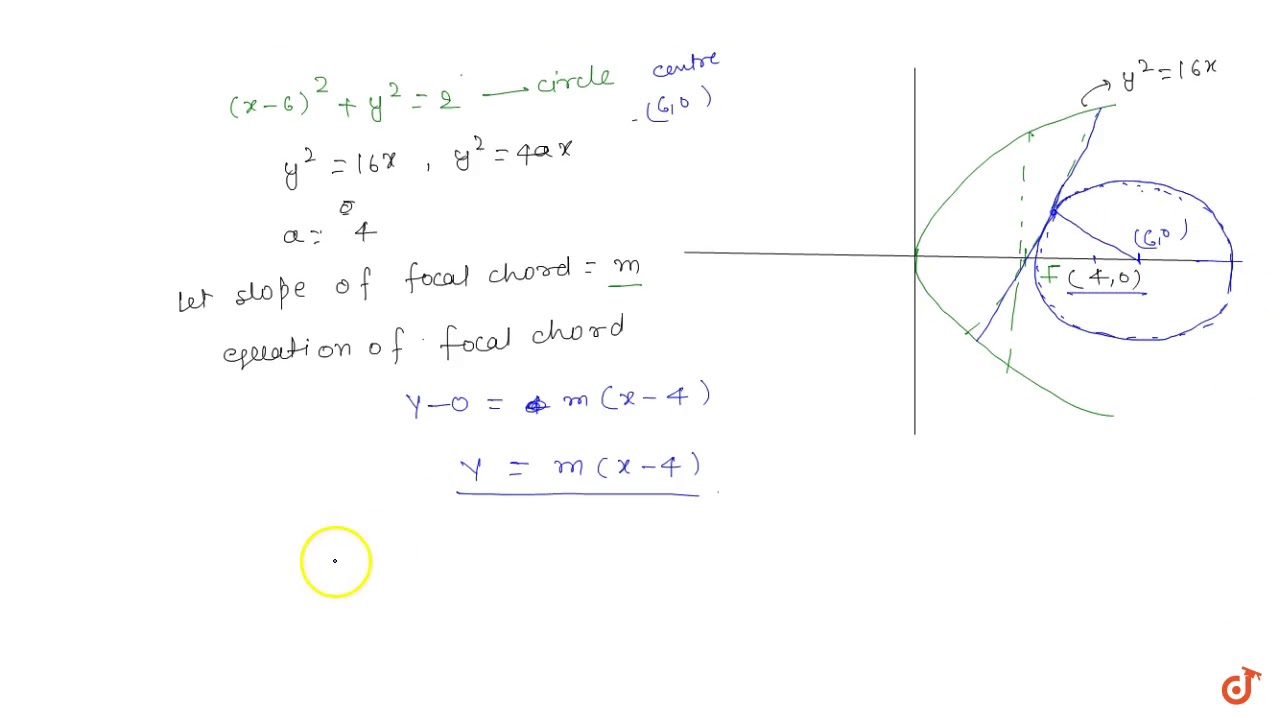



The Focal Chord To Y 2 16x Is Tangent To X 6 2 Y 2 2 Then The Possible Values Of The Youtube



Solution Find The Vertices And Foci Of The Hyperbola Draw The Graph Y 2 25 X 2 21 1 X 2 9 Y 2 16 1



Find All Pairs X Y Of Real Numbers Such That 16 X 2 Y 16 X Y 2 1 Sarthaks Econnect Largest Online Education Community




Solution 4x 2 Y 2 16 Is The Equation Of A An




4 X 2 2x Y 2 8 4 Example 6 Classify A Conic Classify The Conic Given By 4x 2 Y 2 8x 8 0 Then Graph The Equation Solution Note Ppt Download



Solution Y 2 16 X 2 9 1 Identify The Curve Find The Center Asymptotes Foci Then Sketch The Curve




15 Factorise 16x2 See How To Solve It At Qanda




Warm Up Y 8x 2 16x 10 Roots A 8 B 16 C 10 Axis Of Symmetry B 2a X 16 2 8 1 Y 8 1 2 16 1 10 18 Vertex Minimum Ppt Download



Tangent And Normal Are Drawn At P 16 16 On The Parabola Y 2 16x Which Intersect The Axis Of The Parabola At A And B Respectively Sarthaks Econnect Largest Online Education Community




The Graph Of The Function Y 16x 2 8 A 5 X 7a 5 Is Strictly Above




The Graph Of The Function Y 16x 2 8 A 5 X 7a 5 Is Strictly Above




Misc 18 Area Of Circle X2 Y2 16 Exterior To Parabola



Show That X 4 Y 3 X2 16 Xy 12 Y2 9 X3 64 Y2 27 Hence Find The Value If X 3 Y 1 Mathematics Topperlearning Com 8446
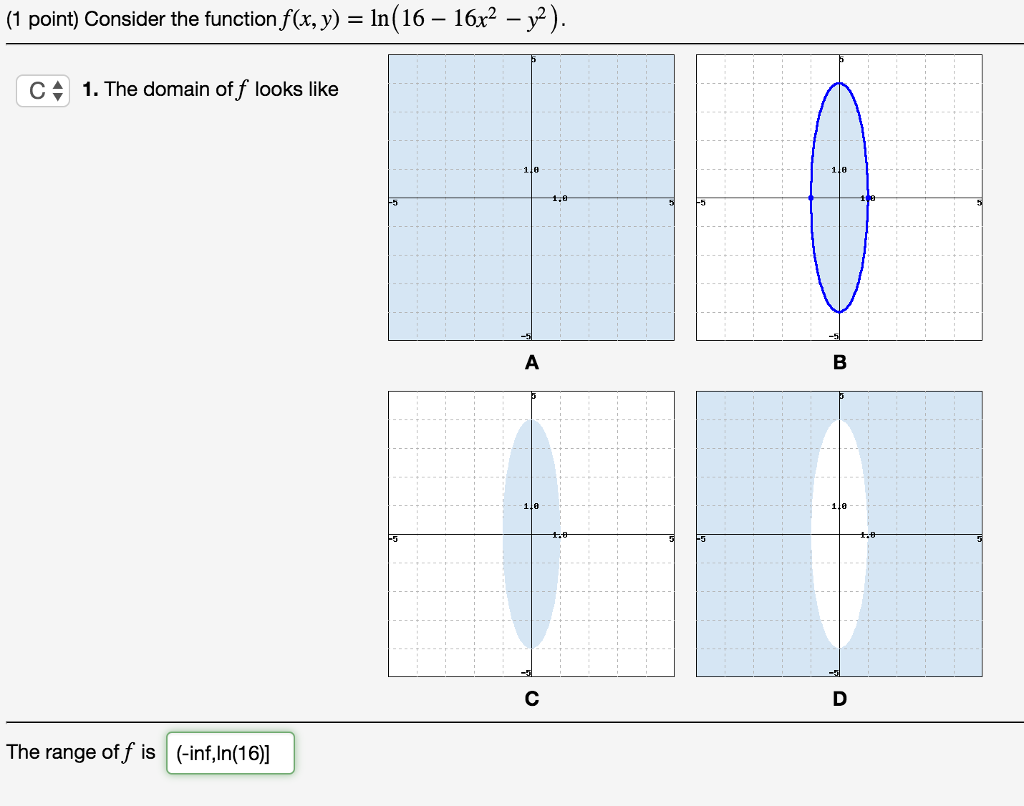



Consider The Function F X Y Ln 16 16x 2 Y 2 Chegg Com
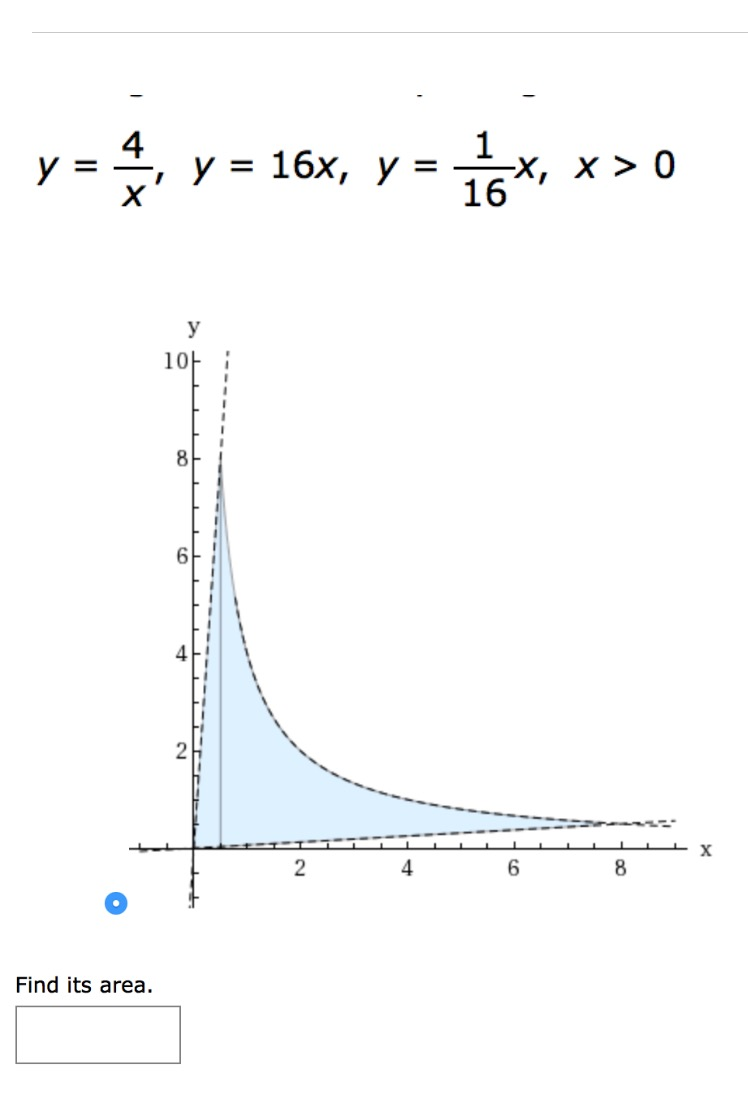



Y 4 X Y 16x Y 1 16 X X 0 Find Its Area Chegg Com
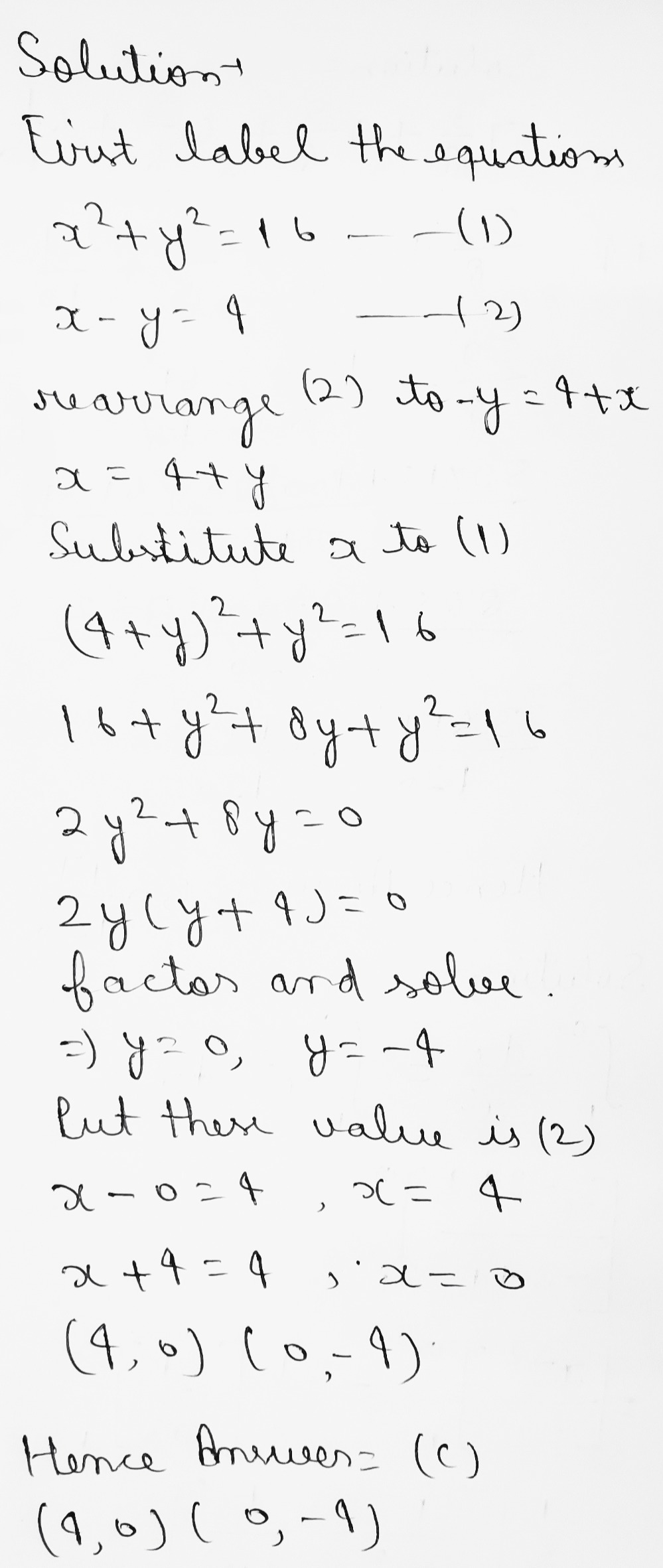



44 Find The Exact Solutions Of The System Of Equat Gauthmath




The Level Curves Of The Function F X Y 16x 2 Chegg Com




The Equation Of Projectile Is Y 16x 5x 2 4 Find The Horizontal Range Sahay Lms
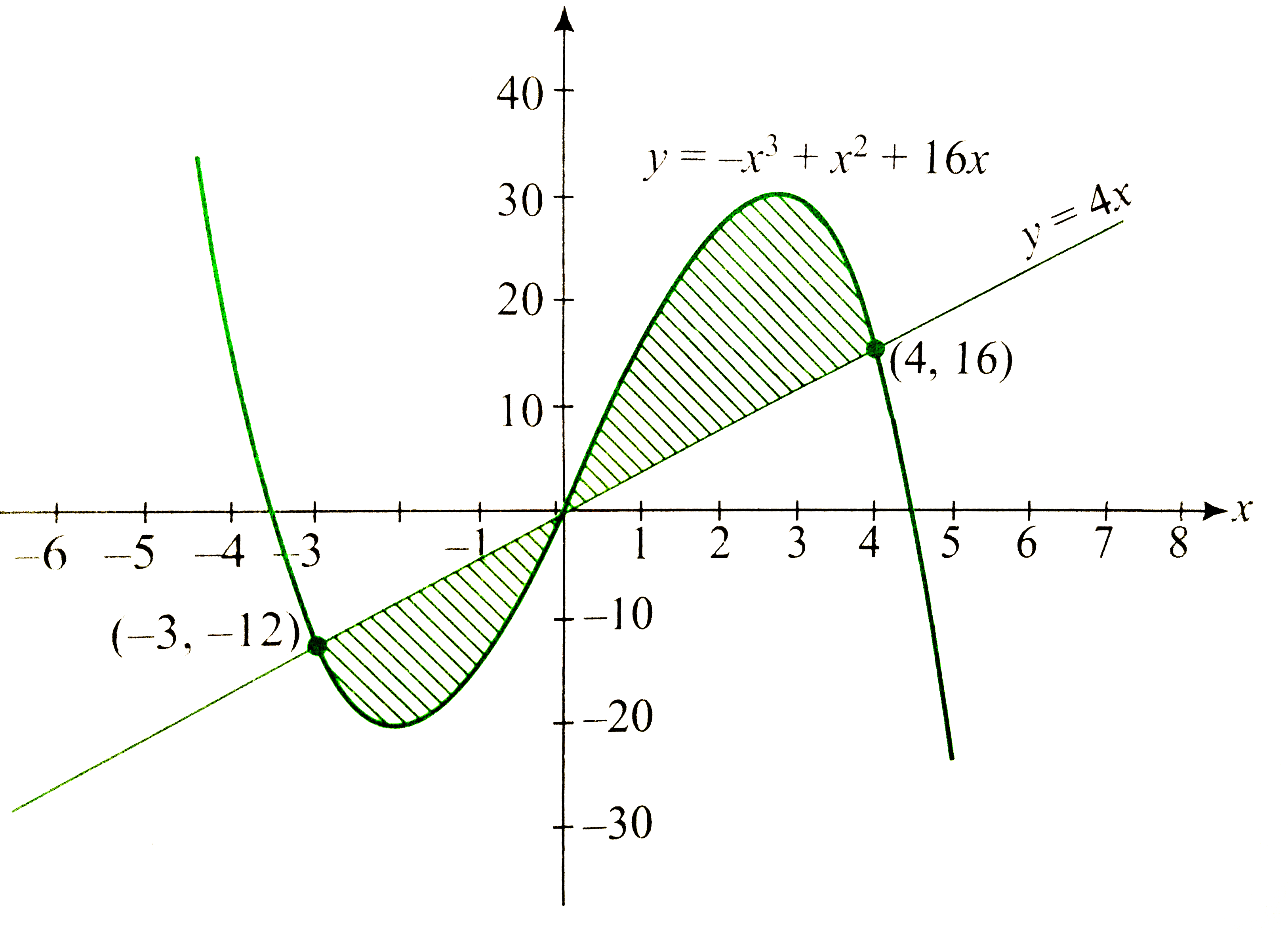



Find The Area Bounded By Y X 3 X 2 16x And Y 4x




Algebra 2 First Semester Final



What Is The Mid Point Of Chord 2x Y 8 0 Of Parabola Y 2 16x Quora



What Is The Area Bounded By The Curve Of Y X 2 And Y 16 Quora
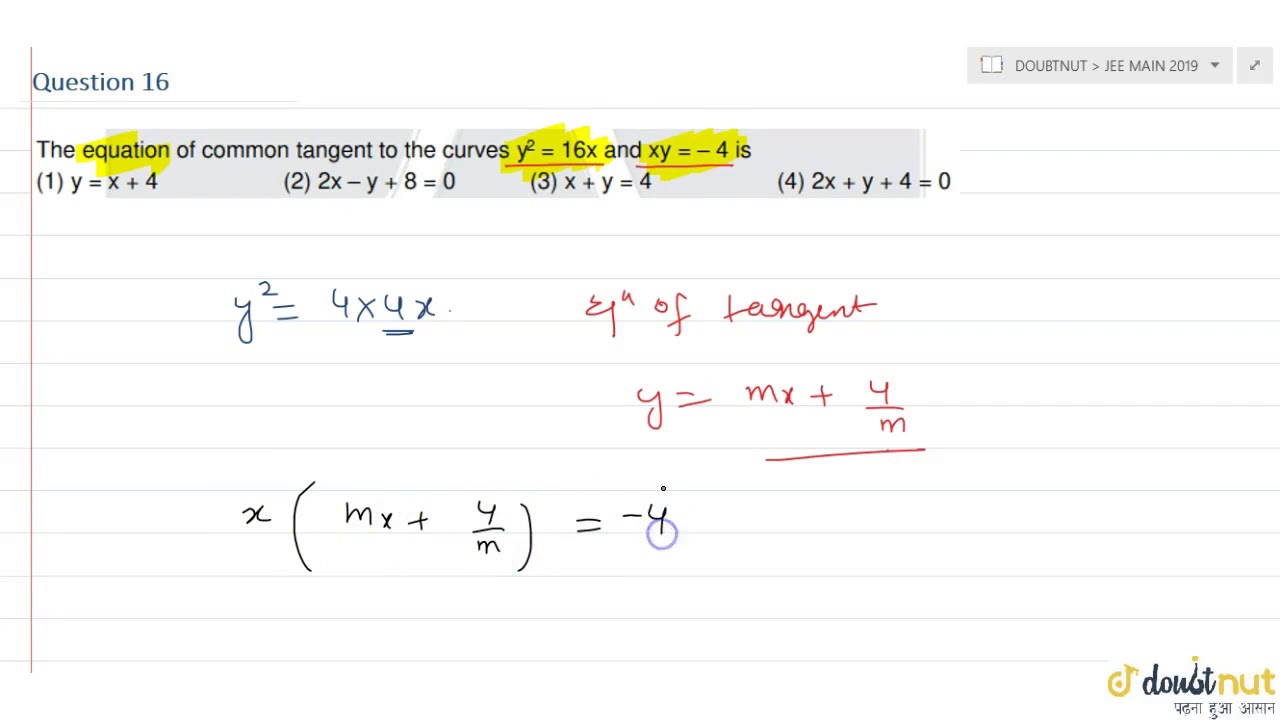



The Equation Of Common Tangent To The Curves Y 2 16x And Xy 4 Is Youtube



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora




Solution Find The Equation Of The Directrix Of The Parabola Y 2 16x



16x 2 4y 2 32x 16y 32 0 Find The Ellipse Mathskey Com
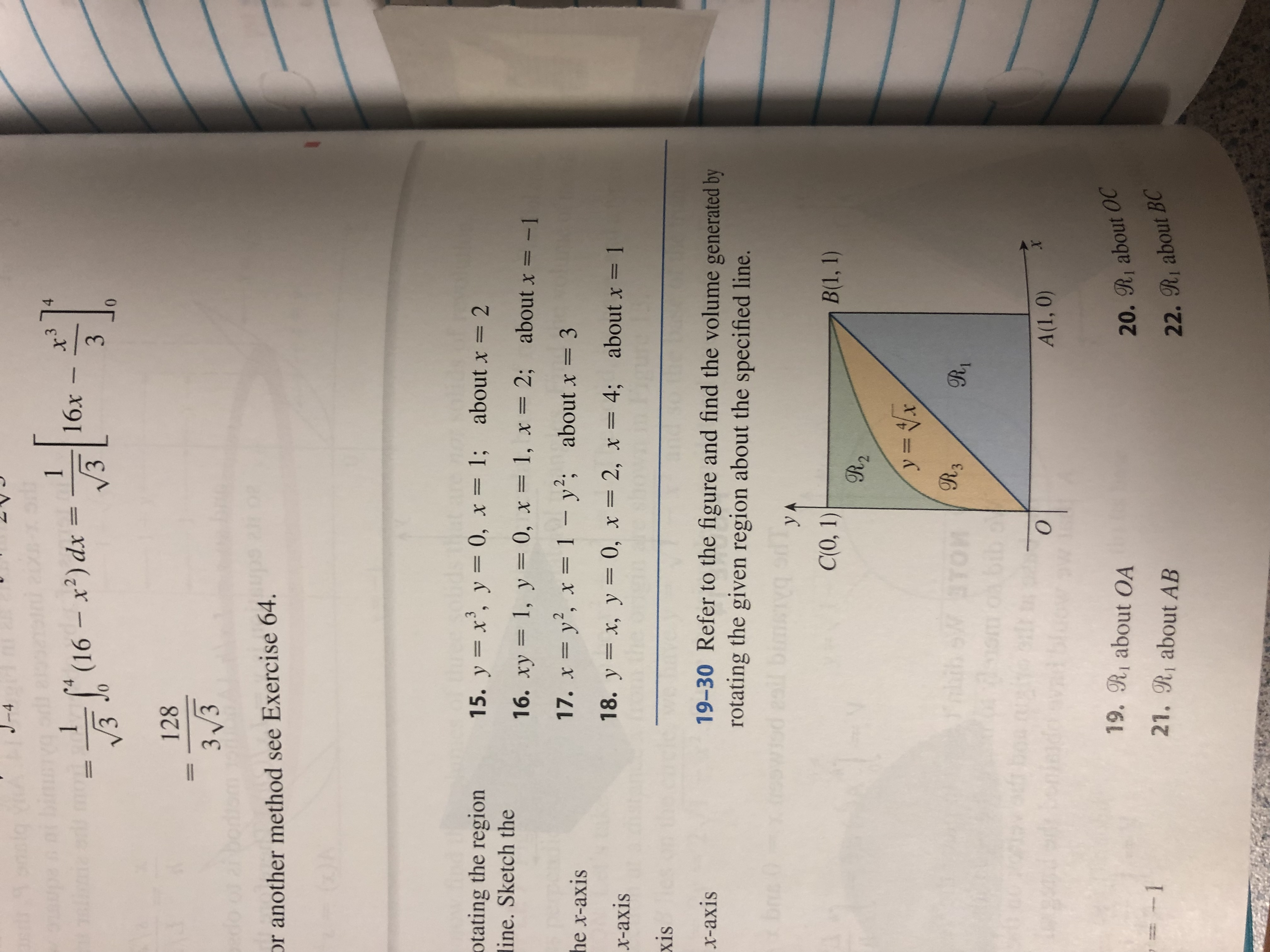



Answered J 4 1 16x 1 16 X2 Dx 3 3 0 128 3 Bartleby




Sketch The Surface Whose Equation Is 16x 2 Y 2 16z 2 4 Study Com




Answered 6 Try Again You Have Answered 1 Out Of Bartleby




Answered 16 Y X X Bartleby
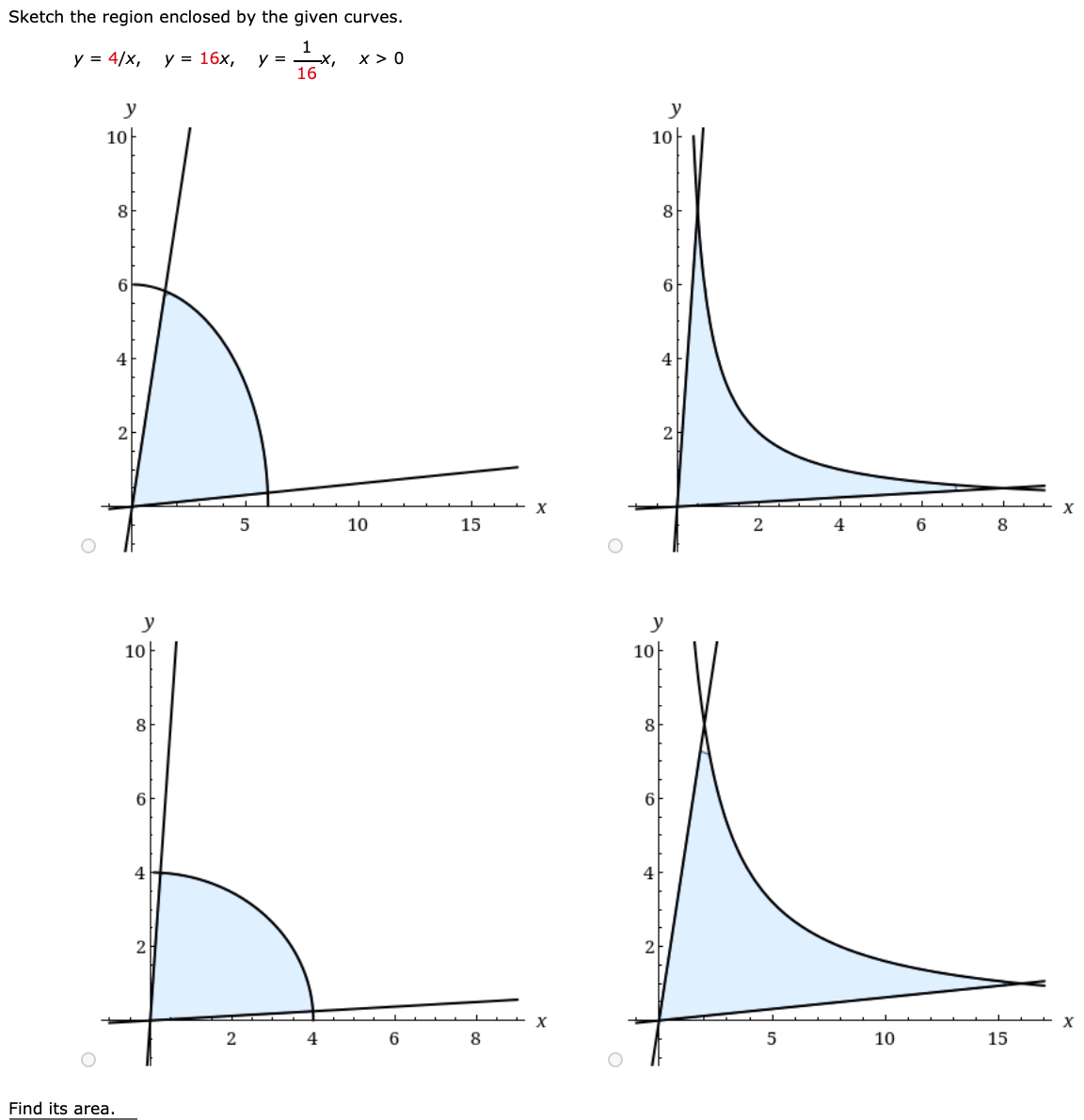



Solved Sketch The Region Enclosed By The Given Curves 1 Chegg Com



Which Equation Is The Inverse Of Y 16x2 1 O Y T6 X 1 O Y 16 Oy Avto Inx 1 Oy Brainly Com




Example 6 Classify A Conic Ppt Video Online Download
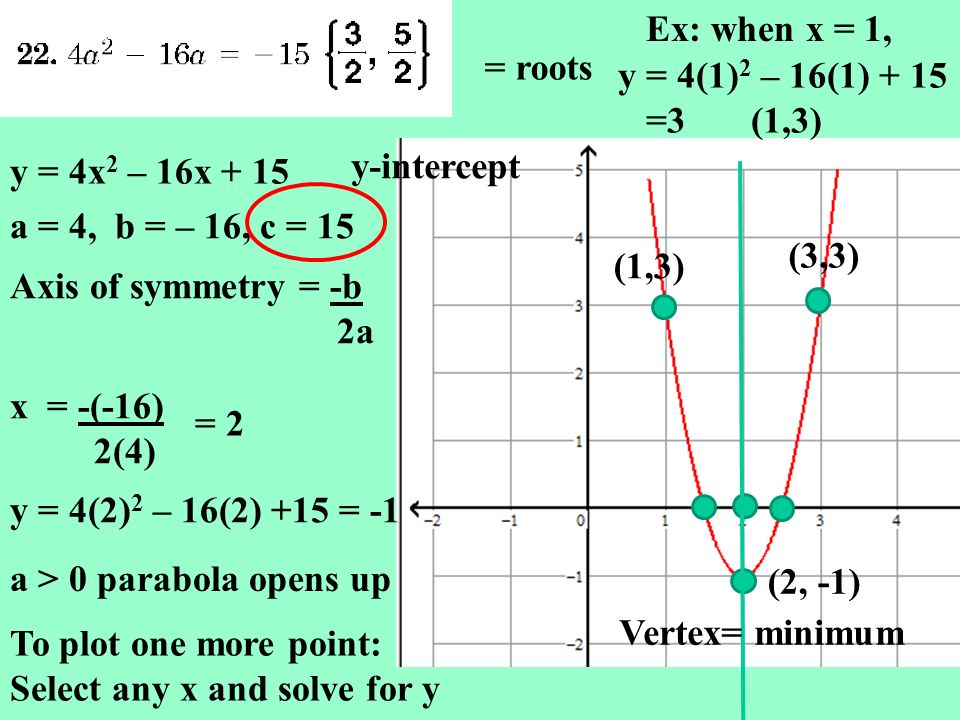



Warm Up Y 8x 2 16x 10 Roots A 8 B 16 C 10 Axis Of Symmetry B 2a X 16 2 8 1 Y 8 1 2 16 1 10 18 Vertex Minimum Ppt Download




Find The Number B Such That The Line Y B Divides The Region Bounded By The Curves Y 16x 2 And Y 9 Into Two Regions With Equal




A Find The Volume Of The Solid Obtained By Rotating The Region Bounded By Y 16x And Y 2x 2 About Y 0 B Find The Volume Of The



Solved Classify Each As Circle Quadratic Parabola Or Other X 5 2 Y 2 2 16 X 2 Y 2 100 Y 2 X 25 X 2 2 Y 5 2 10 Y 2 X 5 Comple Course Hero
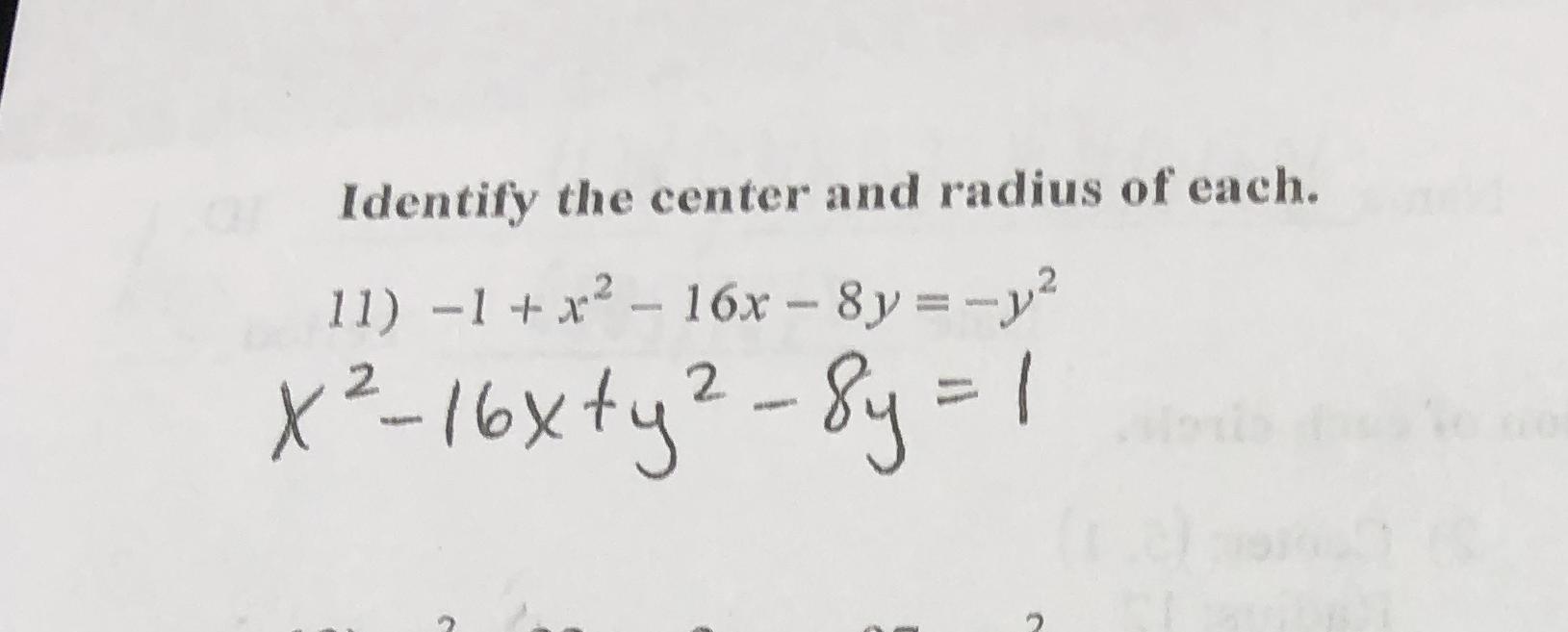



Tify The Center And Ydius Of Each 4 Math X 12 16 X Y 2 8 Y 1 Math Homework Help And Answers Slader



2
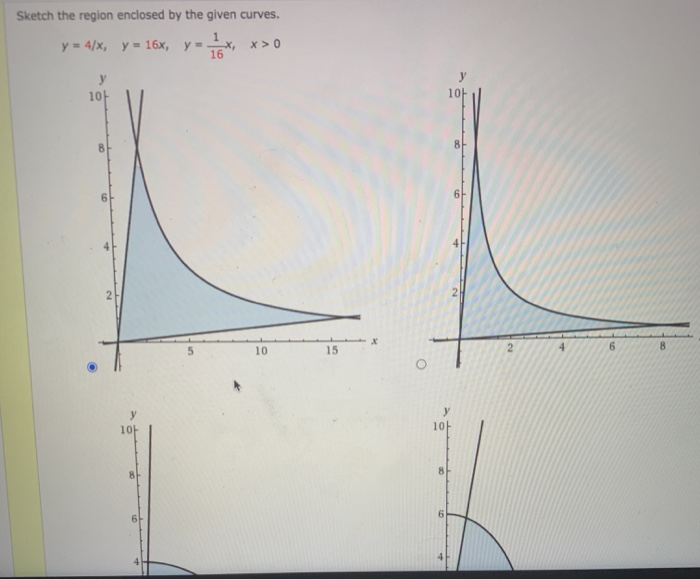



Solved Sketch The Region Enclosed By The Given Curves Y Chegg Com




Find The Area Of The Region Bounded By The Parabola Y 2 16x And The Line X 3



If X Y 16 And Xy 55 What Is The Value Of X And Y Quora



Find The Point On The Parabola Y 2 2x That Is Closest To The Point 1 4 How Can I Approach This Quora




The Equation Of A Tangent To The Hyperbola 16x 2 25y 2 96x 10




Find Inverse Of 2x 2 16x 31 And Write Restricted Domain And Range Youtube




The Eqn Of Projectile Is Y 16x X2 4 The Horizontal Range Is Brainly In



1
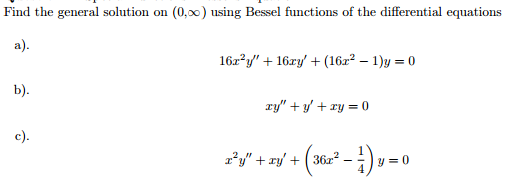



Find The General Solution On 0 Infinity Using Chegg Com




Find The Coordinates Of The Foci The Vertices The Length Of Major Axis The Minor Axis The Eccentricity And The Length Of The Latus Rectum Of The Ellipse 16x2 Y2




Ex 11 3 8 16x2 Y2 16 Find Vertices Eccentricity Ex 11 3




Determine The Inverse Of The Equation Y 16x 2 1 Brainly Com




Math 9 Flip Book Pages 151 0 Pubhtml5



1
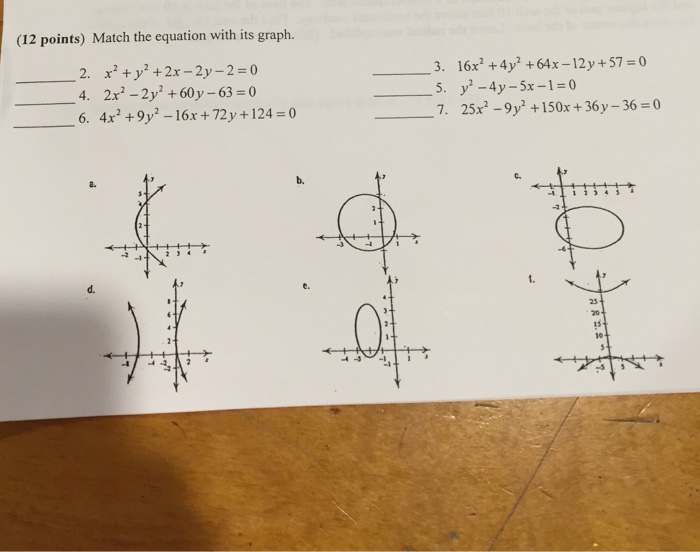



Match The Equation With Its Graph 2 X 2 Y 2 Chegg Com




Solve The Pair Of Linear Equations X Y 16 0 And X 2y 2 By Substitution Method Solve This I Will Follow Brainly In
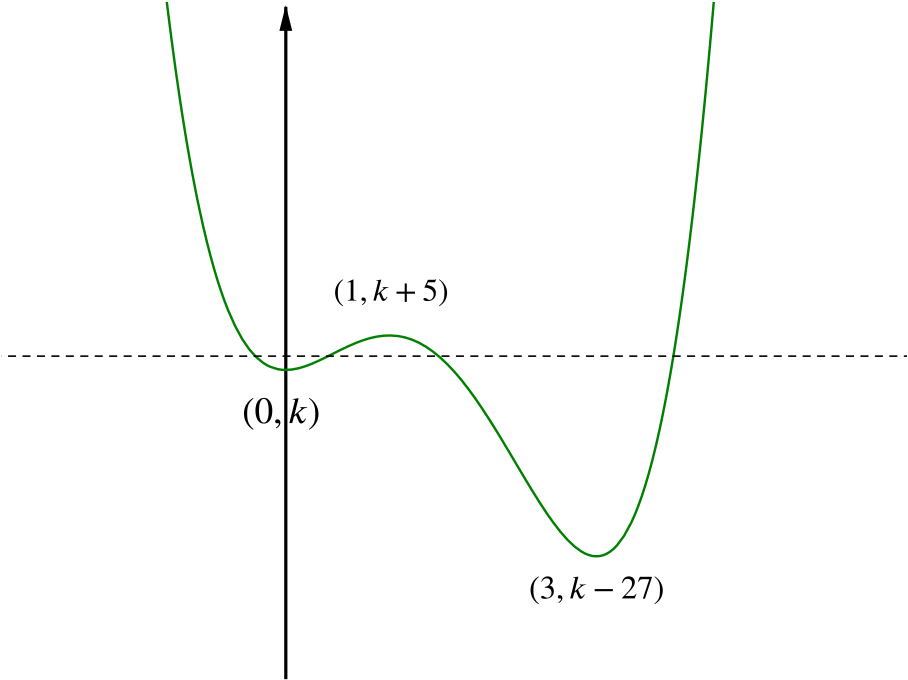



Solution When Does 3x 4 16x 3 18x 2 K 0 Have Four Real Solutions Calculus Meets Functions Underground Mathematics




Systems Of Equations With Substitution Y 5x 8 10x 2y 2 Video Khan Academy




Example 3 Find The Point On The Parabola Y 16x That Chegg Com




Foci Of The Ellipse 16x 2 25y 2 400 Are Youtube




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange




Sketch The Region Enclosed By The Given Curves Y Chegg Com




Ex 11 3 8 16x2 Y2 16 Find Vertices Eccentricity Ex 11 3




31 Equation Of The Tangent To Y2 16x Which Is Perpendicular To 2x Y 5




Misc 18 Area Of Circle X2 Y2 16 Exterior To Parabola




16 X Y 2 X Y 1 8 X Y 12 X Y 7 Solzve The Simultaneous Equation Brainly In



X 2 Y 2 16 Find The Foci And Vertices Of The Ellipse Youtube



Surface Area



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



If X Y 10 And X Y 16 What Is The Value Of X Quora



Solution X Y 16 X Y 2 What Is The Solution Of This System



0 件のコメント:
コメントを投稿